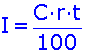INTERÉS SIMPLE

Comenzamos con la segunda parte de la matemática financiera, para ello tenemos que tener bien sabido el tema de porcentaje visto en el capítulo anterior.

Se llama interés simple a la operación financiera donde interviene un capital, un tiempo predeterminado de pago y una tasa o razón, para obtener un cierto beneficio económico llamado interés.

Ejemplo: Calcular el interés producido por un capital de 5000 $ colocado durante

3 años al 9 % anual.

C = 5000 $ T = 3 años R = 9 % ut = 1 año

por lo tanto >>>>>>>>>> I = 5000 . 9 . 3 = 1350 $

100 . 1

aclaración: la unidad de tiempo es el valor numérico de la frase que aparece en la razón

ejemplo : razón 4 % anual representa:

1 año = 12 meses = 2 semestres = 3 cuatrimestres = 4 trimestres = 6 bimestres = 360 días

El tiempo dado T y la razón deben tener las mismas unidades antes de sacar cuentas

Ejemplo : Un capital de 4000 $ es colocado al 5 % mensual durante 3 bimestres, calcular en interés ganado:

C = 4000 $ R = 5 % mensual ut = 1 mes T = 3 bimestres = 9 meses

I = 4000 . 5 . 9 = 1800 $

100 . 1

La matemática financiera comienza luego de este tema a utilizar una fórmula reducida de interés simple con el objeto de poder llegar a deducir otras más complejas, por lo tanto se realizan las siguientes modificaciones:

tasa >>> i = R período >>>> n = T

100 ut

ahora se reemplazan la tasa ( i ) y el período (n) en la fórmula primitiva :

La fórmula principal queda reducida a I = C . i . n

MONTO : Es el capital colocado más es interés ganado

M = C + I

Combinando ambas fórmulas >>>>>>>>>> M = C + C . i . n

Factoreando (factor común, inversa de la propiedad distributiva) >>>>>>>>>>>>>

>>>>>>>>>>>>>>>>>>>> M = C . ( 1 + i . n )

Ejemplos:

EJERCICIO UNO : Un capital de 5000 $ se colocan en un banco al 4% mensual durante 8 bimestres. Indicar el valor del interés y del monto.

Primero se debe “arreglar” los tiempos……………R = 4 % mensual

T = 8 bimestres = 16 meses

Luego si R = 4% entonces i = 0,04

Al estar los tiempos convertidos el Tiempo es igual al período “n” ……….n = 16

Entonces >>>>>>>>>> I = C . i . n = 5000 . 0,04 . 16 = 3200 $

El monto será >>>>>> M = C + I = 5000 + 3200 = 8200 $

En este caso se podría hallar también con la otra fórmula:

M = C . ( 1 + i .n ) = 5000 . ( 1 + 0.04 .16 ) = 5000 . ( 1 + 0,64) = 5000 . 1,64 = 8200 $

EJERCICIO DOS : Un capital de 800$ se transformó en 850 $ en 2 bimestres.

Calcular la tasa mensual.

C = 800 $ M = 850 $ por lo tanto I = 50 $ T = 2 bimestres = 4 meses.

I = C . i . n

50 = 800 . i . 4

50 = 3200 . i

50 / 3200 = i

0,015 = i

Esto significa que la tasa mensual es 0,015 o la razón 1,5 % mensual

3) Un cierto capital se transformó en 25000 $ en dos trimestres, si se aplicó un 3 % mensual. ¿Cuál fue el capital inicial ?

C = x ( hay que averiguar) M = 25000 $ T = 2 trimestres = 6 meses

R = 3 % i = 3 /100 = 0, 03

Con estos datos la única fórmula capaz de resolver el problema es:

M = C . ( 1 + i . n )

25000 = x . ( 1 + 0,03 . 6 )

25000 = x . ( 1 + 0.18 )

25000 = x . 1,18

25000 / 1,18 = x

21186,44 = x >>>>>>>>>>>> C = 21186,44 $

4) Indicar el tiempo en que estuvo colocado un capital de 3000 $ que al ser depositado con una tasa anual de 0,09 obtuvo una ganancia de 400 $.

T = x n = x C = 3000 $ i = 0,09 anual I = 400 $

Este problema puede resolverse con la fórmula:

I = C . i . n 400 / 270 = n

400 = 3000 . 0,09 . n 1,4814 = n

400 = 270 . n

Este número está expresado en años ( ya que la tasa así lo indica ), vamos a transformarlo en un tiempo más real, para ello se debe interpretar lo siguiente:

1, 4814 años = 1 año + 0,4814 año = 1 año + 0,4814 x 12 meses =

= 1 año + 5,7768 meses = 1 año + 5 meses + 0,7768 meses =

= 1 año + 5 meses + 0,7768 x 30 días = 1 año + 5 meses + 23 días

Otros ejemplos:

1) Un cierto capital se transformó en 4600 $ en 4 cuatrimestres, si se aplicó un 1% mensual. ¿Cuál fue el capital inicial y el interés ganado ?

2) Hallar el porcentaje aplicado a un capital de 800 $ para transformarse en 700 $

3) Indicar el valor del capital que al ser colocado al 5 % bimestral durante 3 años produjeron un monto de 6900 $.

4) Un capital de 640 $ sufre un aumento del 20 % y luego un descuento del mismo valor, hallar el monto final.

5) Un capital de 900 $ se transforman en 980 $ en un año. Calcular el interés, la razón y la tasa bimestral.

6) Un hombre coloca 500 $ en un banco que le paga un 4 % bimestral en un año, luego retira la cuarta parte del monto y lo coloca en otro banco al 5 % bimestral durante medio año, con la plata que le sobraba gasta un 40 % en pasajes y un 30 % en indumentaria. ¿cuánta plata le queda para emprender el viaje?

7) Calcular el tiempo que estuvo depositado un capital de 500 $ si se obtuvo una ganancia de 30 $ al ser colocado al 6% bimestral.

8) Indicar el porcentaje de aumento final que sufre un producto si valía 400 $ y le fueron agregados tres aumentos consecutivos del 10 % cada uno.

9) Se depositan 4000$ el 1 de marzo y se retiran el 31 de julio. Si la razón era del 4 % bimestral. Calcular el interés y el monto.

10)Calcular el tiempo que estuvo depositado un capital de 4000 $ si se obtuvo una ganancia de 500$ al ser colocado al 6% anual.

Al invertir un dinero o capital durante un cierto tiempo, nos devuelven ese capital más los beneficios ó intereses. Cuando la inversión es a interés simple los intereses obtenidos se retiran periódicamente y se reinvierte el capital.
La fórmula mas conocida de interés simple es:

Si C es el capital invertido, r el rédito y t el tiempo en años, los intereses producidos I vienen dados por :

donde I es el interés o dinero a cobrar o pagar

C es el capital o dinero a considerar

R es la tasa o razón

T es el tiempo pactado de la operación

ut es la unidad del tiempo considerado.

Si el tiempo no viene dado en años, hay que pasarlo a años, por ejemplo t meses = t/12 años, t días = t/365 años.